Index |
Last Chapter |
Next Chapter |
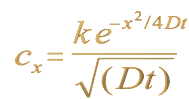
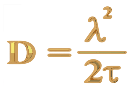
Since they travel about through void, atoms must move on either by their own weight or randomly by the stroke of another. For when during motion they have, as often happens, met and clashed, the result is a sudden rebounding in an opposite direction...
In order to simulate the self-assembly of organic molecules, it will be necessary to model their motion within liquid . Modelling the motion of molecules is, however, an involved process. This chapter conducts a broad overview of physical chemistry, and how it applies to the modelling of liquids, in preparation for Chapter 5 which explicitly covers the model used in this computer simulation.
As the first step in understanding liquids it is necessary to examine the behaviour of gasses, and derive various laws which can then be applied to the liquid case.
The motion of molecules in gases has been studied in great detail, and the theory of particle motion, which can be used to explain the temperature, pressure and density characteristics of a gas, was one of the great triumphs of nineteenth century physical chemistry.
The "Ideal Gas" can be considered to be made up of molecules moving in straight lines, that only interact when they collide. From this simple model, a great many general features of gases can be derived, such as pressure and temperature, and even more complex attributes such as the rate of diffusion.
Unfortunately, for many real gases, this simple model breaks down. It fails in extreme conditions (i.e. high densities and pressures) when the gas starts to display liquid properties, and the assumption the theory makes - that molecules interact only at the instant of collision - fails. More importantly though, it is inaccurate for all but the simplest molecules, even under standard conditions, due the energy of the molecule not being confined to the kinetic energy of linear motion. Instead, the collision energy is absorbed by the molecule in a number of different ways, being spread between kinetic energy, rotational energy and vibrational energy. In extreme conditions it is also absorbed in electronic transitions within the component atoms of the molecule.
A further complication is the quantum nature of the inter-molecular interactions. Quantum theory and experimental observations show that certain energy-related molecular attributes can adopt only discrete, rather than continuous values. The four attributes of interest to us are linear momentum (kinetic or "translational" energy), angular momentum (rotational energy), vibration (vibrational energy), and the energy of electronic transitions. Energy transfers between molecules occur only in discrete amounts that depend on the values of these four attributes.
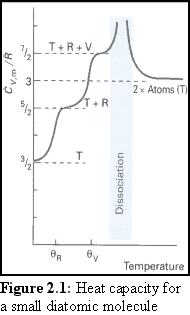
Although molecules in any but the smallest containers have an effectively continuous range of allowable kinetic energy values, this is not the case for the other energetically excitable modes of the molecule. Rotation, vibration and electronic transitions are all quantised in a way that affects their behaviour under normal conditions. If we want to model the behaviour of colliding molecules, we need to understand the quantum nature of molecular interactions.
As a broad but useful generalisation one can think of these four different "modes" of energy storage becoming "active" under different conditions. At absolute zero (0 K), each mode of the molecule is at its lowest possible energy, known as its "ground state". This implies that all the molecules in a sample are stationary, not rotating, not vibrating, and all of the electrons in each molecule are at their lowest possible electronic level. As the molecules heat up, a significant number of molecules will leave the ground state for these four modes. Once a significant proportion of the molecular population has left the ground state for a particular mode, the mode is said to have become 'active'.
The first mode to become active is the translational energy mode. This activation is caused by the molecule's straight-line motion. Technically this mode is quantised, but in fact in all but the smallest containers and at the lowest temperatures the possible energy levels are so close as to effectively form a continuum, so that the molecule can adopt almost any velocity.
As the temperature increases, the rotational modes of a molecule are the next to become active. Here the energy levels are not so closely spaced and it takes greater energies for the higher levels to become populated.
As the molecule continues to gain energy, the vibrational modes become active. The activity of this mode can be worked out by approximating the force field that the molecule's component atoms experience due to each other. Since they have a greatly restricted space, they are relatively highly quantised, and the allowable energies are further apart than for the rotational modes.
Finally, with increased heating, the electronic mode becomes active. The quantum equations governing this activation mode can be complex and difficult to solve for any but the very simplest molecules. However, it can be predicted that because the electrons have relatively little room to move, and are also very light, they have greatly separated energy levels, and this is indeed what is found experimentally.
At the point where one particular mode is just starting to become active, there will be only a small number of (quantised) energy levels for that mode, and it is necessary to work them out precisely. If, for example, the rotational states of a small molecule at cryogenic temperatures were being considered, it would be necessary to explicitly examine each possible rotational state. But once a sufficient number are active, there are useful approximations that can be made which greatly simplify the analysis of the gas, especially if an aggregate is considered in place of an individual molecule.
Once the energy levels that are available to a molecule are known (either theoretically or from experimentation) it is possible to obtain the "Boltzmann distribution", which describes statistically the most probable configuration of energies of all the particles in a gas. This shows, for example, the distribution of translational energy in a gas at a given temperature, which is equivalent to describing the average speed, and speed distribution, of a gas. (This special case of the Boltzmann distribution is better known as "the Maxwell distribution".)
The Boltzmann distribution describes more than just the distribution of speeds in a population; it can predict the distribution of all energy modes, be they translational, rotational, vibrational or electronic.
A useful result that can be derived from the Boltzmann Distribution is that, when there are a large number of available energy levels the 'equipartition principle' may be used to work out how much energy is bound up in each mode.
The equipartition principle simply states that, provided there are a large number of populated
energy levels available in a given mode, each active mode in a molecule will have a mean energy
of ![]() , where k is the Boltzmann constant and T is the temperature. Thus all energy is 'equally
partitioned', spread evenly across all possible energy modes. For a typical gas molecule, this
might be three velocity modes (representing motion in the x, y and z directions) and two active
rotational modes (for a diatomic molecule say, where the third rotational mode
, where k is the Boltzmann constant and T is the temperature. Thus all energy is 'equally
partitioned', spread evenly across all possible energy modes. For a typical gas molecule, this
might be three velocity modes (representing motion in the x, y and z directions) and two active
rotational modes (for a diatomic molecule say, where the third rotational mode
is not yet active). The mean energy of each molecule would then be ![]() (since there are five
available modes to absorb energy).
(since there are five
available modes to absorb energy).
From this equation it is possible to compute the mean velocity of molecules in a gas, and also the mean rotational energy of these molecules. At very high temperatures, the mean vibrational and even electronic mean energies may be determined in this manner.
It is a feature of quantum mechanics that the larger the molecule is, the more closely spaced are its quantised energy levels. Therefore, rather than working out the energy levels explicitly for large molecules, at normal laboratory conditions ('Standard Temperature and Pressure', being 105 Pa and 298.15 K ), the Boltzmann distribution and the equipartition principle can be used to closely estimate the energies involved in movement and rotation.
This technique is used later in this thesis to justify the treatment of the angular motion for large molecules.
In an ideal gas, particles can be thought of as solid spheres in constant motion, continually ricocheting off each other in an endless succession of elastic collisions. In such a gas, the motion of each particle follows a 'random walk', also known as Brownian motion or a 'drunkard's walk'. The particle moves a short random distance (usually considered to be on the order of 10s of nanometres (5)) before colliding with another particle, and rebounding in a random direction.
Over time, the probable position of the particle is found to approximate a Gaussian distribution (covered in detail in chapter 5). The continual collisions, and the particle's velocity, cause the particle to be bounced away from its starting position. It is still most likely to be found in this general region, but it may have been bounced further afield. The interesting feature of this motion is that while the particles may have a large velocity, the actual distance travelled from their starting position may not be very great, due to the large amount of backtracking the particle may have done. Hence, even in a high temperature gas where the gas molecules are moving very quickly, the actual change in position of a particle over time may be only a small fraction of the distance travelled. There is a graphical representation of this (shown in a different context) in figure 5.2 of Chapter 5.
This random walk applies also to particles in a liquid, and heavy use of it is made to model motion in the simulator developed in later chapters. As well as emerging from a consideration of the motion of individual properties, the random walk can also be derived from consideration of the diffusion properties of large-scale aggregates of molecules. (cf. Appendix A for a detailed treatment of molecular motion.)
Liquids are obviously very different from gases. In the ideal gases considered so far all interactions are rigid, inelastic collisions, with unconstrained motion between collisions.
In a liquid though, the molecules are in almost continuous interaction with their neighbours, via electrostatic forces such as dipole or van der Waals forces (6). In order to move, a molecule in a liquid must break away from at least some of its neighbours. But in doing so it will immediately fall under the influence of another molecule, and so on.
Another effect of this semi-continuous interaction is that the particles in a liquid are far more closely packed than in a gas. As a result, the motion of a liquid particle before it is involved in a collision with another particle (the "mean free path") is much shorter than it would be in a gas, even ignoring the longer range inter-molecular electrostatic forces.
The large scale effect of this semi-continuous interaction on a particle is, however, the same as in a gas. The particle moves in a random walk, although the "steps" of the random walk are much smaller, being on the order of 100pm for small molecules instead of 100nm for a small gas molecule (7). At the smallest scale, in a liquid paths are not even entirely straight, due to interactions with neighbouring particles. But the end result is identical: particles move in a random walk through the liquid, diffusing slowly to move to new positions that are far less distant from their original position than their raw velocities would suggest.
Completely modelling the particles of a liquid is a very complex and computationally intensive task. Since the component molecules all interact with each other almost continuously, modelling a liquid in detail requires far more computation for a given number of molecules over a fixed period of time than for a gas (where the interactions are more infrequent).
Some computer simulations of liquids attempt to carefully model the trajectories of all the interacting particles, by plotting their motions as the particles move through the potentials of their neighbouring particles; a method called "molecular dynamics". In order to be accurate, the time steps for such simulations must be very short, with complete recomputations of the entire system occurring on the order of femtoseconds. This is less than the average time between collisions, but allows the non-linear trajectories of the particles to be more accurately modelled. The result is still, unfortunately, an approximation, since it is an example of the Newtonian many-body problem which (generally) has no exact solution, but if the time step is made sufficiently small, it can be a very good approximation. Even more detailed simulations modelling the quantum mechanics of small systems can be created, but require a supercomputer to simulate a small number of atoms.
This method would be completely impractical for this thesis, where the intention is to simulate reactions occurring on the order of seconds. Even on the fastest supercomputer available in 2000, such simulations would be impossible using this method.
This approach is more like the one used in this thesis, but at a much smaller scale. Each particle in the simulation is moved by a small, random amount, and the potential energy of the new configuration of molecules is calculated. Whether the new configuration is accepted, or whether another random position is generated for the particle, depends on the likelihood of the new configuration. In effect, if the new configuration is unlikely, dice are rolled to see whether or not it will be accepted. This procedure is repeated for all the molecules, and for numerous time steps, to build up a model of the liquid. The advantage of this more abstract method is lower computational requirements.
The complexity of the problem can be greatly reduced if, rather than considering all the solvent molecules, only the smaller number of solute particles are considered. In fact, if the size of the solute molecules is sufficiently larger than that of the solvent molecules, the solute particles can simply be considered as moving in a constant density fluid, rather than in a sea of discrete particles. This approximation greatly simplifies the problem.
In order to model the solute molecules at a molecular level, it is necessary to know how their motion varies, depending on such interrelated factors as temperature, the mass and shape of the particle, the viscosity of the medium, and the frictional coefficient of the molecule. All this data is summarised by the diffusion constant, which describes how quickly molecules of a certain type will diffuse through a solution. From this, the measurable diffusive macro-behaviour of a chemical species, the mobility of an individual molecule can be found. (This mobility can also be theoretically approximated, see Chapter 5.)
The motion of a large molecule within a solvent is again found to be a random walk, and the diffusion constant allows the characterisation of the molecule's motion as a Gaussian distribution, representing the probability that at some given time in the future the particle will be at a particular position. This approximation holds so long as the chance of interaction with another, similar particle is not great. Since the concentration of solute particles, especially when they are macromolecules, is usually quite small, it is possible to model correspondingly larger time steps during computer simulation, often on the order of microseconds. This is nine orders of magnitude longer than the time steps required for molecular dynamics.
Modelling rotational motion, although a little more difficult from a practical point of view, is in theory very similar to modelling linear motion. Whereas linear motion deals with position, velocity, force, mass, and acceleration, rotational motion deals with angular position, angular velocity, torque, moment of inertia and angular acceleration. In many respects the angular properties are direct analogues of the linear ones, and equations such as "force equals mass times acceleration" become "torque equals moment of inertia times angular acceleration".
The equipartition principle can be used to estimate the statistical distribution of the rotational energy in a group of molecules. Combining this with a molecule's moment of inertia provides the rotational velocity distribution, which can then be used to describe the movement of the molecule. The moment of inertia is easily calculated, as is the centroid, (or centre of rotation) of the molecule.
Unfortunately, although this approach works well for a gaseous molecule, it is less accurate for one suspended in a liquid. A molecule in a liquid is not free to rotate without interference from neighbours, and in fact liquids generally display 'short range order', where the local neighbourhood of a liquid molecule displays a crystalline, solid-like structure, that rapidly degrades. For example, water displays short-range order at the level of individual water molecules similar to that found in ice; it is simply that the structure is imperfect, and the molecules constantly moving, that keeps water from being a solid. If the degree of molecular movement is slowed by cooling, this short range order becomes greater and greater, until the liquid freezes.
Even more complex is the case of a macromolecule. In the most common solvent, water, macromolecules are surrounded by a layer of ordered water molecules known as a 'hydration sphere' (or more generally, a 'solvation sphere') - which increases its effective size to the 'hydrodynamic radius', which must also be taken into account in linear motion. The hydration sphere hinders the macromolecule's rotational motion, as do large non-spherical deviations in the macromolecule's shape. These features make it difficult to predict the macromolecule's rotational behaviour, which is also difficult to measure directly. The effect can be partially compensated for by using a larger volume when calculating theoretical figures, and by using experimental data where possible.
When two molecules collide it is possible they will react together. Unfortunately, determining exactly the conditions and probabilities of a reaction, especially for larger molecules, is a very difficult task, and usually resort is made to direct experiment. But, once experiment has determined values for one set of conditions, they can often be extrapolated to other circumstances.
The theory, in its simplest form (8), simply treats the molecules of a gas as having both a collision cross-section (the size of the particle used for calculating if it is hit by another particle), and a 'reaction cross-section' related to the collision cross-section by a 'steric factor'. The steric factor is usually much less than 1, and might be interpreted as expressing the fact that reaction is probabilistic: particles that collide have a chance of reacting, but do not necessarily do so.
The theory can be extended to liquid reactants, but again heavy reliance must be made on experimental work. Hence, in the models developed in this thesis (where possible) the values for interaction are obtained by reference to experimentally obtained data.
Index |
Last Chapter |
Next Chapter |
1. The material in this chapter is a summary of undergraduate level Physical Chemistry, and a large number of excellent texts exist. The most complete is: Atkins, P.W., Physical Chemistry, 5th Ed. (1994), OUP, Oxford.
2. Also good is Chap 1-6 of Pascoe, K.J., Properties of Materials for Electrical Engineers, (1973) John Wiley & Sons, Bristol.
3. Also Chap 1-5 and 15-21 of Chang, R. Physical Chemistry with Applications to Biological Systems (1981), Macmillan, New York
4. Image from Atkins op. cit., p 707
5. The actual distance, so long as it is small on the time and distance scale being considered, is not actually very important. It is usually assumed (e.g. Atkins op. cit. p 855) for a liquid to be on the order of a small molecular diameter, e.g. 210pm for an SO42- molecule, and would be less for a large molecule. Hence for simulations dealing in nanometres, the Brownian motion approximation is valid for all molecules in liquid. For a gas the distance is much greater, e.g. 70nm for N2 at room temperature (Atkins op.cit. p 40).
6. Pascoe, K.J. op cit., P 76
7. These are obviously only orders of magnitude figures, since actual values will vary greatly depending on molecular size, temperature, pressure etc. See Atkins op. cit. chapter 1.
8. Atkins, op. cit., chap 27