Index |
Last Chapter |
Next Chapter |
Herba mala cito crescit
(An evil plant grows quickly)
- Roman Proverb
Writing a program to model the behaviour of assembling actin and tubulin is challenging, but once it is created the same principles can be applied to other self-assembling nano-scale structures. The use of program input files (the ".pddf" files - cf. Appendix C) means that different proteins and other organic molecules, and possibly even inorganic objects, can be modelled without having to modify the original nanoscale simulator program.
To perform such simulations accurately requires detailed experimental measurements of the chemical and physical properties of such objects, especially details such as binding energies between each component type, which are beyond the scope of this thesis. Without such measurements, though, it is still possible to investigate the geometry and general behaviour of various hypothetical structures, composed of different types of building blocks with differing geometrical relationships to each other. This chapter outlines a number of geometric structures as a proof of concept, before attempting in broad terms to model the capsid construction of a "typical" virus - herpes simplex A.
Regular solids are some of the easiest objects to model, since their geometric relationships with each other are simple to determine mathematically.
The five platonic solids (the four-sided tetrahedron, six-sided cube, eight-sided octahedron, twelve-sided dodecahedron and twenty-sided icosahedron) are straightforward to model. The icosahedral form is especially interesting since, as will be seen later, the coat protein capsid sheath of many viruses is icosahedral in nature. Pddf files are presented for cubes, dodecahedron and icosahedrons in Appendix D: The Platonic Solids.
The dodecahedron is a twelve sided solid, each side of which is a pentagon. It can be modelled easily using identical monomeric subunits, each of which has five possible linkage sites (Fig. 9.1, Table 9.1). The linkage sites are represented as the base of the green arrows in figure 9.1, while the direction of the links is indicated by the arrows themselves.
Note that there is a geometric similarity between the icosahedron (Table 9.2), with twenty faces and twelve corners, and this dodecahedron, with twelve faces and twenty corners. As a result this same subunit is later used for the "corner" subunit of an icosahedral viral shell.
A simulation run with monomers of this sort produces twelve unit aggregates, as shown in figure 9.2. Free monomers are in red, aggregated monomers in blue. Note the partially assembled dodecahedrons in the background.
The icosahedron is a 20-sided object, each side of which is a triangle. It can be modelled easily using identical monomeric subunits, each having three possible linkage sites (Table 9.2).
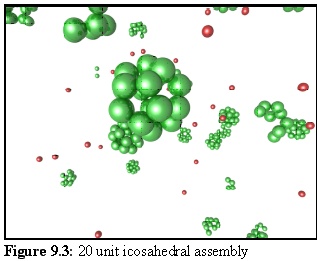A simulated sea of such monomers produces twenty unit aggregates, as shown in figure 9.3. Free
monomers are in red, aggregated monomers in green. Note the partially assembled icosahedral
aggregates in the background. Also note how having the monomer units in the centre of each face gives
rise, as a consequence of the geometry, to an open structure where the faces of each icosahedron are
surrounded by five spheres.
Many objects form infinitely repeating regular structures, including some proteins that, in purified form, will condense into regular crystals that can be used for X-ray diffraction and other experimental techniques that take advantage of the periodicity of such crystals. Since the nanoscale simulator operates primarily on the level of the individual object, no special programming is needed to allow the modeller to simulate the growth of such crystals. But because the physical chemistry of the interaction of the objects is being approximated with the concept of "linkage sites", the interactions between growing crystal regions that result in cleavage planes are not strongly modelled.
A simple 2-D sheet can be grown using a monomer with three linkage sites placed in a plane with 120 degree separation angles (Table 9.3). Such a sheet grows indefinitely, eventually wrapping around the simulation volume to meet itself (recall that a particle that leaves one 'side' of the simulation volume immediately re-enters on the opposite side).
Although it would be theoretically possible for the sheet to meet itself and bind (forming in effect a 3-dimensional torus with a 4-dimensional twist), in fact the program does not handle this situation very reliably because internal checks, that prevent an aggregate colliding with itself, trigger warnings. In general, one part of an aggregate should never collide with another part of the same aggregate during normal movement, so the program treats any such collision as an error condition. But, although the program currently fails in this (rare) limiting case, aggregates up to the size of the simulated field size are easily handled. The .pddf file for this 2-D lattice is given as the example file in Appendix C, Protein Dynamic Description Files.
2-D sheet growth could be used to simulate the assembly of the flat sheets of actin or tubulin that can be grown under certain experimental conditions (1).
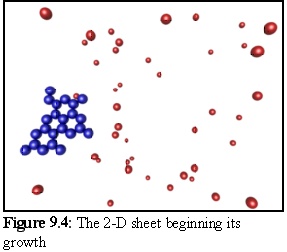
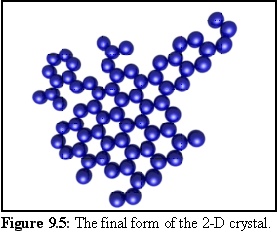
Using this geometry for monomers, the following structures were produced in a simulation run. The probability of initial nucleation is deliberately set low, so that only one structure is likely to be created. When a nucleation event finally occurs (Fig. 9.4), the structure grows quickly until all available free monomers are bound (Fig. 9.5).
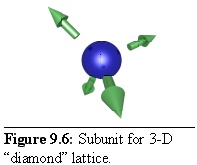
In the same way a three-dimensional crystal can be formed, using a repeating subunit with three-dimensional links. For example, a "diamond-like" tetrahedral lattice can be constructed by using subunits with four links, spaced so as to form the edges of a tetrahedron (Fig. 9.6):
In order to make the structure a little more obvious, the spherical particles have been modelled at a smaller radius than their linkages, hence the gap between the sphere surface and the base of the arrows, representing the link sites. This also leads to the final structure being an "open" lattice, with space between components (Table 9.4).
The resulting structure formed during simulation (Fig. 9.7) is difficult to interpret visually, in part due to the number of lattice defects in the form of missing subunits. (The set of binding rules used to construct this model favoured rapid growth, leaving a number of holes in the structure as the aggregate grew.) The crystalline structure is still apparent in the ordered rows of objects that can be made out running approximately perpendicular to the page:
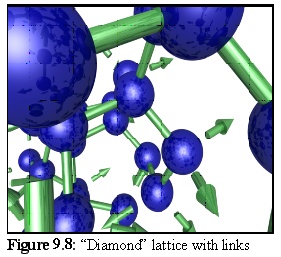To get a better idea of the structure, a section of the above lattice is shown (Fig. 9.8) with links (and unfilled linkage sites) (2).
The .pddf file representing this structure is given in Appendix E, "Tetrahedral Lattice .pddf File".
Some of the most complex and interesting self-assembling structures found in cells are in fact viruses that have invaded from the outside, and are using the machinery of the cell to reproduce themselves. Although a number of types of viruses exist, one common type involves a hard proteinaceous shell in an icosahedral shape, known as the capsid, surrounding the fragile viral DNA. In broad terms, the shell protects the viral DNA when the virus is outside the cell, and once the virus enters a new cell this outside sheath is removed, allowing the viral DNA to begin replicating itself, producing more viral DNA and capsid proteins.
It appears that these capsid proteins are capable of self-assembling into completed capsids without help from external scaffolding proteins, although the exact details of the process are not yet fully understood. If this is the case, then viruses are among the most complex self-assembling proteinaceous structures in the cell, with a typical virus shell having hundreds of individual capsid subunits (3).
Simulating the method by which a virus is constructed is a difficult undertaking, requiring a careful understanding of the molecular nature of the viral coat proteins, and is well beyond the scope of this thesis. But as an example of future directions, the following section outlines how such an exercise might be conducted using a program such as the nanoscale simulator. The example studied is a simplified model of the Herpes Simplex A virus, based heavily on the work of Zhou et al. (4), (5), (6), (7). Herpes Simplex A was selected as an example of a well studied virus of intermediate complexity.
Shortly after the work described in this thesis was performed, some excellent work (already referred to in Chapter 5) was published by Schwartz et al. (8), building on earlier work by Berger et al. (9). They showed that mathematical rules, at an individual capsid level, could determine virus structure as well as explaining some experimentally observed defects.
The system of mathematical rules used by Berger et al. operates on the theory that viral capsids are not necessarily of distinct types (neither chemically different, nor chemically similar but with a different conformation), but rather it assumes that capsids can assume different conformations, with different binding properties, depending on their neighbours at the time of binding. This rules based system included a model of the energy involved in each link, and iteratively optimized forces and torques within the system to arrive at a final structure. From this model a number of interesting results were obtained, especially in studying models of viral mis-formation, where even a single incorrect addition leads to a malformed capsid (10).
It should be noted that this premise, that different capsids change conformation depending on the type of binding they undergo, may not be a complete description for all viruses. The work of Zhou et al., which forms the basis of the work later in this chapter, describes the viral capsid assembly of HSV-1 (herpes simplex) in terms of capsids that, althoguh similar, are in fact structurally different, being made up from slightly different arrangements of (shared) basic subunits (11), (12).
In the later (Dec. 1998) paper Schwartz et al. extended the 'local rule-based theory' to a kinetic simulation similar in some respects to that presented in this thesis. The authors combined the detailed modelling of intra-aggregate forces with a simple model of Brownian motion to simulate a sea of up to 300 particles, using a powerful 8-processor computer. In order to obtain results quickly they used a very high concentration of 247 M to create a model of a generic T=1 capsid virus assembly in a simulation of 25,000 time steps. Due to the deliberately abstracted nature of the simulation, there was no attempt to obtain a time scale.
The authors of this latest paper derive a number of interesting results related to the degree of tolerance that can be allowed in the links between capsids before viral capsid assembly fails. They also demonstrate a modelling system which provides a considerably more detailed model of the intra-aggregate forces than is attempted in this thesis.
While the details of aggregates are modelled in depth, the larger-scale modelling of the local-rule based system is highly abstracted, which leads to a number of shortcomings.
One of the strengths of the Schwartz model is the detail with which intra-aggregate forces are modelled. However this comes at a great computational price - the simulation runs performed were of the order of 300 particles x 25,000 steps. In comparison, the actin simulation of Chapter 7, on a substantially slower computer, modelled 1,600 particles x 100,000 time steps, in a volume 500 times larger. While the nanosimulator is faster, it is at the expense of this detailed modelling of forces within the aggregate, and it is likely a combination of the two techniques would be rewarding.
Despite the effort Schwartz et al. have gone to in representing collisions in terms of binding energies, it appears that it is still necessary to employ various (apparently) ad-hoc angular and distance tolerances for potential bonds. As these presumably affect the probability of collisions that may lead to binding opportunities, they effectively modify the basic probabilities that have been determined based on association activation energies.
In conclusion, as the only other major work in the area of simulating the self-assembly of large numbers of proteins from a simulated solution of free monomers that this author is aware of, the viral assembly work of Schwartz et al. Offers valuable insights that in many ways complement the work described in this thesis. Whereas this thesis spends most of its effort on the large scale problems of dimer and aggregate movement and collision, and optimising algorithms for speed, the virus assembly work of Schwartz et al. concentrates on the fine detail of how individual aggregates behave, and abstracts the larger scale details. It would be advantageous if the two approaches could be combined, and there is no reason to think that they could not. The software architecture and .pddf language of the nanoscale simulator allows for this type of conformational change on binding, and associated local rule system, although it has not been implemented.
Herpes Simplex A is a complex "T16" icosahedral virus (the T16 refers to its geometric structure; it means it is an icosahedral virus, with each "face" consisting of 15 subunits, with units on the edges being shared with other faces). Its structure, as described and illustrated by Zhou et al. on their webpage (13) is made up of "protein subunits in ... three distinct morphological units: penton, hexon and triplex of this T=16 icosahedral particle". They present the illustration reproduced in figure 9.9:
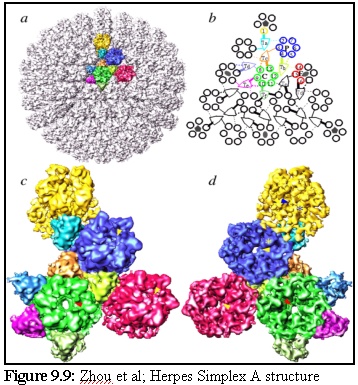
and the following descriptive text:
" (a) The whole capsid is shown as shaded surface with the structural components in one asymmetric unit in color. Included in an asymmetric unit are morphological components from penton (yellow), P-hexon (blue), E-hexon (red), C-hexon (green) and six different types of triplex (other colors). (b) The schematic diagram of one triangular face of the herpes virus capsid illustrates the interactions between the subunits (VP5) of penton and hexons (1 - 16) and triplexes Ta, Tb, Tc, Td, Te and Tf. Subunits within an asymmetric unit are shown using the same color coding as in (a). Four kinds of interactions between triplex and VP5 are depicted, including strong head (thick solid line), weak head (thick dashed line), tail (thin solid line) and arm (thin dashed line). (c) The contiguous group of morphological components colored in (a) is blown up and shown as viewed from outside (c) and inside (d) respectively. Arrowheads in (c) indicate the contacts between triplexes and their adjacent penton and hexons. Only those visible at this view are indicated." (14)
To summarise the above description, the major capsid proteins are of four main types:
In addition, there are a large number of much smaller proteins that join these larger components together, the "triplexes".
Although a full simulation would include the triplexes, in this discussion they are ignored, and only the larger pentons and hexons are modelled, along with some simplified rules of association that can all be deduced from the relationships described above.
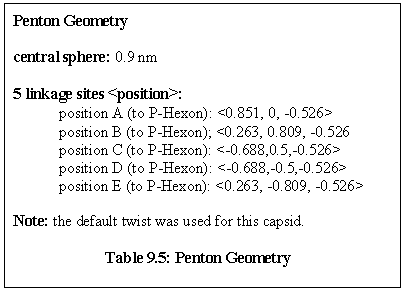
The geometry of the structure is somewhat involved. The relative positions of the capsids were carefully worked out by hand (as with all the other structures presented in this chapter), but a complication arises with the linking behaviour. When an object binds another object, their new orientation is specified by the 'twist' vector parameter of the link (cf chapter 6, "Binding Free Objects"). The twist vectors were also carefully worked out, on geometrical grounds, to ensure that when capsids bound to other capsids they were correctly oriented. Sometimes the program default twist was adequate (if no twist vector is specified, the program calculates the twist as being at right angles to the link direction, in the same plane as the z-axis), while at other times it had to be specified directly. All link directions were calculated so that capsids would bind collinearly.
An overview of the structure of the capsid proteins follows, and complete details of the .pddf file are given in Appendix F.
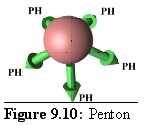Rules: The Penton's five links each bind to one site only on a P-Hexon.
Role: The Penton is the vertex unit of virus.
(Note: In figure 9.10 and following images the links are labelled with the destination type, using the following abbreviations:
P = Penton;
PH = P-Hexon, or "Penton Adjacent Hexon";
EH = E-Hexon or "Edge Hexon";
CH = C-Hexon or "Centre Hexon". )
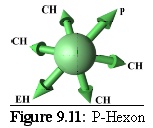Rules: The P-Hexon has one link that binds to a Penton. The two links adjacent to that bind to other P-Hexons. The link opposite the Penton link binds to an E-Hexon, and the two adjacent links bind to C-Hexons.
Role: The P-Hexon is an edge unit, lying adjacent to the Penton. ("Penton associated, or adjacent, Hexon".)
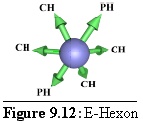Rules: Two opposite links bind to P-Hexons, the others all bind to C-Hexons.
Role: The E-Hexon is the other edge unit, lying in the very middle of an edge between two P-Hexons. ("Edge Hexon".) Its geometry is identical to that of the P-Hexon although its binding rules differ.
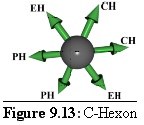Rules: Two adjacent links bind to other C-Hexons, the opposite links bind to P-Hexons, while the other two, diametrically opposing, links bind to E-hexons.
These hexons make up the central three units of a virus face. ("Centre Hexon".)
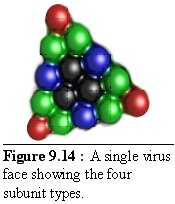
These units fit together to form a virus side as shown in figure 9.14 (the colour coding is the same as above, but the shades are darker). This simplified structure should be compared with figure 9.9 above.
By initialising the nanoscale simulator with a mixture of the hexons and pentons described above, in approximate proportion to their frequency in the shell (a complete shell has 12 Pentons, 60 P-Hexons, 30 E-Hexons, and 60 C-Hexons) the initial conditions are created for viral shell formation. In this simulation, the probability of initial nucleation is deliberately kept low, resulting in a small number of initial nucleation sites, which then grow into full-sized shells with little or no interaction between aggregates.
Since this simulation was intentionally abstract, it was run in a favourable environment. The concentration was relatively high (6.2 M) in a 512nm cubed simulation space (4000 monomers). Binding strengths were made artificially high (0.9 prob of binding), and the simulation was run for less than a second, until reasonably complete structures appeared. The numbers of different proteins was in the following proportions (from the .pddf file:) Penton 8%, HexonP 37%, HexonE 18%, HexonC 37%.
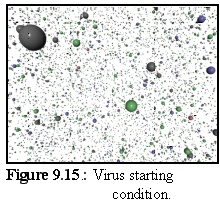
Initially, the four capsid element types are floating free in the simulation (Fig. 9.15):
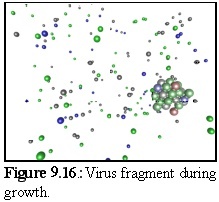
Figure 9.16 shows a close up of a partially constructed virus capsid, currently about half completed.
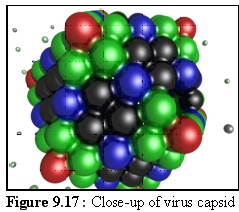
Figure 9.17 shows a nearly complete capsid at close range.
The above is far from an accurate simulation of viral assembly, however it demonstrates the power of the nanosimulator, in that a large number of particles (4,000) of four different protein species were successfully simulated over several thousand time steps, and a complex structure comprised of hundreds of individual units self assembled based only the geometric rules of the four component capsid proteins. As far as the author is aware, this is the first time the assembly of such a geometrically complex aggregate, comprised of different proteins has been simulated.
To improve the simulation, physically reasonable values for the binding and breaking probabilities should be obtained, or at least approximated, and the role of joining proteins (the triplexes) should be included in the model. It is also possible that the viral DNA or RNA itself should be modelled as a physical component that fits within the capsid shell; it might be speculated that it plays a role in the construction of the shell itself, perhaps as a nucleation point for the capsid? (Although it should be noted that viral capsids can self-assemble in-vitro, even without the presence of viral DNA/RNA.)
A further possibility for experiment is adopting the local rule-based model mentioned previously, where instead of four major protein species (and potentially six 'triplex' glue proteins), only one protein capable of adopting different conformations on binding is used (and similarly a single 'triplex' glue protein capable of adopting six conformations). This may well turn out to be a physically more realistic model for many viruses, and is a promising avenue of research.
Modelling viral assembly in this way may be helpful for drug design, since some anti-viral drugs act by disrupting the coat assembly/disassembly process (15). For example, a drug that acted as a nucleation site to produce geometrically inaccurate shells might be useful in disrupting the viral growth cycle, and its effects could be "designed" to an extent using the nanoscale simulator (16).
Having tested the simulator on tubulin and actin, this chapter has shown that the simulator can be applied as a general purpose tool for self-assembling systems.
The nanoscale simulator has been shown to be sufficiently flexible to model a broad range of objects, ranging from small aggregates made up of a single type of subunit, through to very large, complex aggregates such as virus capsids, made up of a number of different types of subunits with different properties. Since the nanoscale simulator uses the same rules and data structures for manipulating all these objects, modelling a new type of subunit simply requires using a different ".pddf" file, and does not require any changes to the central program.
A wide range of different protein species (or other nanoscale objects), each with its own geometry, linkage definitions, and physical characteristics, can be simulated in large numbers over a large number of time steps. Another useful feature is that, in the absence of experimental data, the program will estimate features such as mass, moments of inertia and diffusion coefficients based on average protein density. This allows the nanosimulator to be used for more speculative simulation, while maintaining physically realistic values.
Index |
Last Chapter |
Next Chapter |
1. Amos, L.A. and Amos, B.A. (1991) op. cit.
2. Outputting links is a special simulator feature only available within the output raytracer files.
3. Alberts et al, (1994), Molecular Biology of the Cell, Garland Publishing, New York, Chapter 6 esp pp274-282.
4. Zhou, Z.H., Prasad, B.V.V., Jakana, J., Rixon, F. and Chiu, W. (1994) Protein subunit structures in the herpes simplex virus capsid from 400 kV spot-scan electron cryomicroscopy. J. Mol. Biol. Vol 242, pp456-469.
5. Zhou, Z.H., He, J., Jakana, J., Tatman, J., Rixon, F. and Chiu, W. (1995) Assembly of VP26 in HSV-1 inferred from structures of wild-type and recombinant capsids. Nature Struct. Biol. Vol 2, 1026-1030.
6. Zhou, Z. H., Chiu, W., Haskell, K., Spears, H. J., Jakana, J., Rixon, F. J. and Scott, L. R. (1998). Refinement of herpesvirus B-capsid structure on parallel supercomputers. Biophys. J. Vol 74, 576-588.
7. Zhou, Z. H., Macnab, S. J., Jakana, J., Scott, L. R., Chiu, W. & Rixon, F. J. (1998). Identification of the sites of interaction between the scaffold and outer shell in HSV-1 capsids by difference electron imaging. Proc. Natl. Acad. Sci. USA Vol 75, 2778-2783.
8. Schwartz, R. et al. (1998) op. cit.
9. Berger, B. et al. (1994) op. cit.
10. Prevelige, P.E. Jr., (1998), Inhibiting virus-capsid assembly by altering the polymerisation pathway, Tibtech, Vol 16 pp 61-65.
11. Z. Hong Zhou et al. (1995), Assembly of VP26 in herpes simplex virus-1 inferred from structures of wild-type and recombinant capsids, Nature Struc. Bio. Vol 2, No. 11, pp 1026-1030
12. Trus, B.L., Newcomb, W.W., Booy, F.P., Brown, J.C. & Steven, A.C. (1992), Distinct monoclonal antibodies separately label the hexons or the pentons of herpes simplex cirus capsid, Proc. Natl. Acad. Sci. USA Vol 89, pp 11508-11512
13. See the website http://ncmi.bcm.tmc.edu/Projects/icos/icos.html
14. Ibid.
15. E.g. Badger, J. et al., (1988), Structural analysis of a series of antiviral agents complexed with human rhinovirus 14, Proc. Natl. Acad. Sci. USA Vol 85, pp 3304-3308
16. Prevelige, P.E. Jr., (1998) op. cit.